📘 What are Regression Problems and Their Meaning?
Regression problems are a cornerstone of machine learning and statistics, focusing on predicting continuous numerical values rather than discrete categories. Unlike classification problems that predict labels like 'spam' or 'not spam', regression models forecast real-valued outcomes such as prices, temperatures, or quantities.
Key Characteristics of Regression Problems: • Continuous Output: Target variables are real numbers (e.g., 45.67, 1000.50) • Supervised Learning: Requires labeled training data with input-output pairs • Pattern Recognition: Learns relationships between independent variables (features) and dependent variables (targets) • Error Minimization: Models aim to minimize the difference between predicted and actual values
Real-World Examples: • Financial Forecasting: Predicting stock prices or sales revenue • Weather Prediction: Forecasting temperature or rainfall amounts • Healthcare: Estimating patient recovery time or drug dosage • Real Estate: Valuing property prices based on features • Marketing: Predicting customer lifetime value or conversion rates
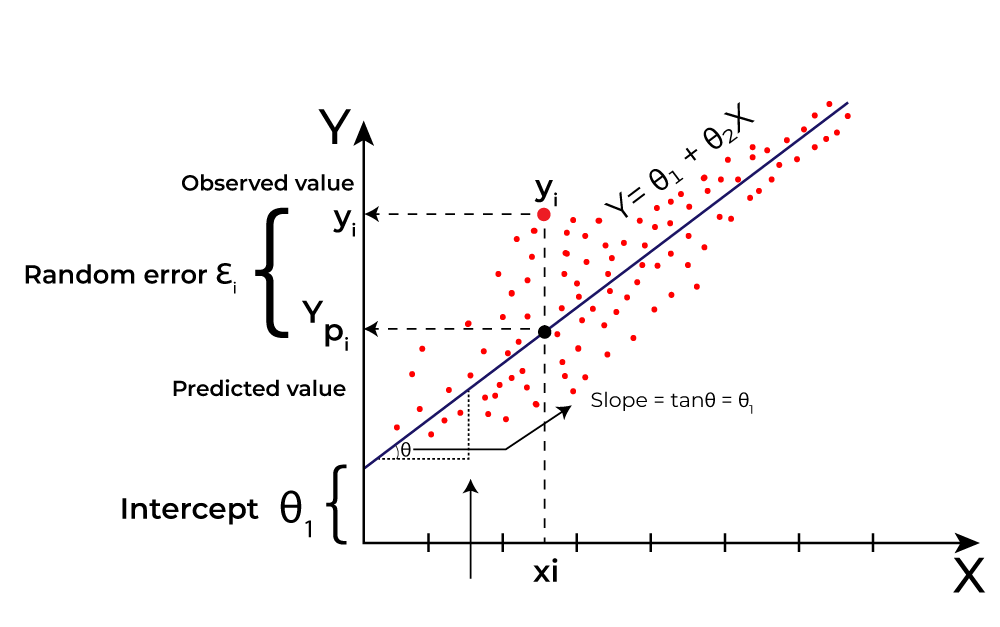
🔍 How Do Real-Value Predictions Happen in Regression?
Real-value predictions in regression involve finding the best mathematical relationship between input features and the target variable. The process typically includes:
1. Data Collection and Preparation • Gather historical data with known input-output pairs • Clean and preprocess data (handle missing values, normalize features) • Split data into training and testing sets
2. Model Selection and Training • Choose appropriate regression algorithm based on data characteristics • Train the model by minimizing a loss function (e.g., Mean Squared Error) • Use optimization techniques like Gradient Descent
3. Model Evaluation and Validation • Assess performance using metrics like R², MAE, RMSE • Validate on unseen test data to prevent overfitting • Fine-tune hyperparameters for optimal performance
4. Prediction and Deployment • Use trained model to make predictions on new data • Deploy model in production environment • Monitor performance and retrain as needed
🤖 Machine Learning Models for Regression Problems
Machine learning offers various regression algorithms, each suited for different types of data and relationships:
1. Linear Regression • Assumes linear relationship between features and target • Simple, interpretable, and fast to train • Best for datasets with linear patterns
2. Polynomial Regression • Extends linear regression to capture non-linear relationships • Uses polynomial features (x², x³, etc.) • Good for curved relationships but prone to overfitting
3. Decision Tree Regression • Builds tree-like structure for predictions • Handles non-linear relationships and feature interactions • Easy to interpret but can overfit
4. Random Forest Regression • Ensemble of decision trees for improved accuracy • Reduces overfitting through averaging • Robust and handles missing values well
5. Support Vector Regression (SVR) • Uses support vector machines for regression • Effective in high-dimensional spaces • Good for non-linear relationships with kernel tricks
6. Neural Network Regression • Deep learning approach with multiple layers • Excellent for complex, non-linear patterns • Requires large datasets and computational resources

📈 What is Linear Regression? Complete Explanation
Linear Regression is the most fundamental and widely used regression algorithm in machine learning and statistics. It establishes a linear relationship between the dependent variable (target) and one or more independent variables (features).
Definition: Linear Regression predicts the target variable as a linear combination of input features, assuming a straight-line relationship between variables.
Key Assumptions: • Linearity: Relationship between features and target is linear • Independence: Observations are independent of each other • Homoscedasticity: Constant variance of errors across all levels • No Multicollinearity: Features are not highly correlated • Normality: Residuals follow normal distribution
Working Principle:
- Model Representation: Y = β₀ + β₁X₁ + β₂X₂ + ... + βₙXₙ + ε
- Parameter Estimation: Find optimal β values using methods like Ordinary Least Squares (OLS)
- Error Minimization: Minimize the sum of squared differences between predicted and actual values
- Prediction: Use learned parameters to predict new values
🧮 Mathematics Behind Linear Regression
The mathematics of linear regression involves finding the best-fit line through data points by minimizing the error.
The Linear Regression Equation:
Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + \dots + \beta_nX_n + \epsilon
Where: • Y: Dependent variable (target to predict) • X₁, X₂, ..., Xₙ: Independent variables (features) • β₀: Intercept (bias term) • β₁, β₂, ..., βₙ: Coefficients (weights for each feature) • ε: Error term (residual)
Cost Function - Mean Squared Error (MSE):
MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2
Gradient Descent Optimization: • Iteratively update parameters to minimize cost function • Learning rate controls step size in parameter updates • Convergence when cost function stops decreasing significantly
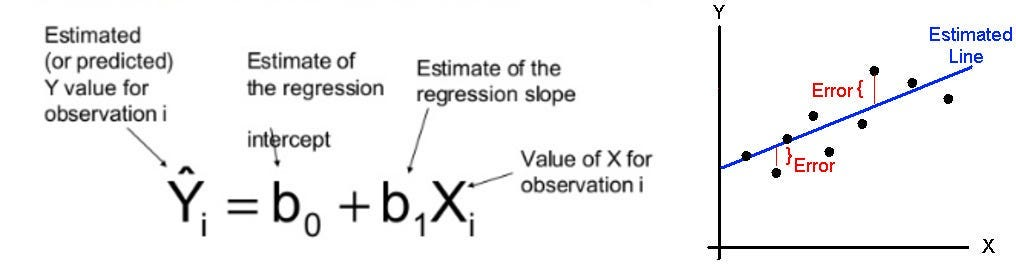
🏠 Practical Example: House Price Prediction with Linear Regression
Let's apply linear regression to predict house prices based on features like size, bedrooms, and location.
Dataset Example: | Size (sq ft) | Bedrooms | Location Score | Price ($) |-------------|----------|----------------|-----------| | 1500 | 3 | 8 | 250000 | | 2000 | 4 | 9 | 350000 | | 1200 | 2 | 7 | 180000 | | 1800 | 3 | 8 | 280000 |
Model Training: • Features: Size, Bedrooms, Location Score • Target: Price • Algorithm: Multiple Linear Regression
Prediction Equation:
Price = -50000 + 120 \times Size + 15000 \times Bedrooms + 20000 \times LocationScore
Implementation Code (Python with scikit-learn):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
# Load data
data = pd.read_csv('house_prices.csv')
X = data[['size', 'bedrooms', 'location_score']]
y = data['price']
# Split data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Train model
model = LinearRegression()
model.fit(X_train, y_train)
# Make predictions
predictions = model.predict(X_test)
# Evaluate
mse = mean_squared_error(y_test, predictions)
print(f'Mean Squared Error: {mse}')
**📂 Complete Code Repository and Jupyter Notebook
For a full hands-on experience with linear regression, including data preprocessing, model training, evaluation, and visualization, check out the complete code repository:
1
https://github.com/zeeshanali90233/MachineLearning---DeepLearning/tree/main/04-Linear-Regression✅ Advantages and Disadvantages of Linear Regression
Advantages: • Simplicity: Easy to understand and implement • Interpretability: Clear relationship between features and target • Speed: Fast training and prediction • No Tuning Required: Few hyperparameters to adjust • Foundation: Basis for more complex algorithms
Disadvantages: • Linearity Assumption: Can't capture non-linear relationships • Outlier Sensitivity: Affected by outliers in data • Multicollinearity: Problems when features are highly correlated • Underfitting: May be too simple for complex datasets • Feature Scaling: Requires proper scaling for optimal performance
🎯 Key Takeaways: Regression Problems and Linear Regression
• Regression Problems involve predicting continuous numerical values using machine learning • Linear Regression assumes linear relationships and is the foundation of predictive modeling • Mathematics includes cost functions, gradient descent, and statistical assumptions • Practical Applications span finance, healthcare, real estate, and many other domains • Implementation is straightforward with libraries like scikit-learn • Evaluation uses metrics like MSE, MAE, and R² score
Mastering regression problems and linear regression opens doors to advanced machine learning techniques and real-world problem-solving!
📚 Resources and Further Reading
• Books: "An Introduction to Statistical Learning" by James et al. • Online Courses: Coursera's Machine Learning by Andrew Ng • Documentation: Scikit-learn Linear Regression docs • Practice: Kaggle regression competitions • Advanced Topics: Regularization techniques (Ridge, Lasso)
About the Author: Zeeshan Ali is a machine learning engineer specializing in predictive modeling and data science. Connect on LinkedIn for more ML insights.